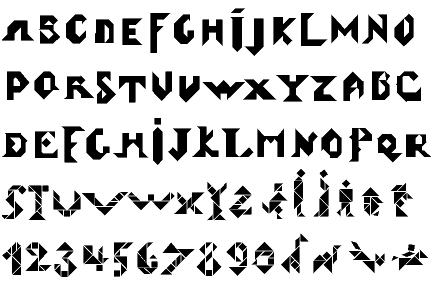O que é Tangram e como surgiu?
O Tangram é um quebra-cabeça chinês formado de sete peças: um quadrado, um paralelogramo, dois triângulos isósceles congruentes maiores, dois triângulos menores também isósceles e congruentes e um triângulo isósceles médio. As sete peças formam um quadrado.Surgiu há mais de 2000 anos e seu nome original, "Tchi Tchiao Pan", significa "Sete Peças da Sabedoria".Seu objetivo é conseguir montar uma determinada forma, usando as sete peças.
Hoje, o Tangram é utilizado por todo o mundo, especialmente por professores no ensino da geometria, matemática, psicologia e, principalmente, na pedagogia. Apesar de passar uma simplicidade no manuseio, ele se revela um jogo de difícil resolução por exigir muito raciocínio lógico.
Existem várias lendas sobre o surgimento do Tangram. Diz algumas escrituras que: uma pedra preciosa se desfez em sete pedaços e com eles era possível formar várias formas (animais, plantas, pessoas) outra diz que um imperador deixou o seu espelho cair, e esse se desfez em 7 pedaços que poderiam ser usados para formar várias figuras. A lenda principal e mais difundida a respeito do surgimento do Tangram diz que no século XII um monge taoísta deu ao seu discípulo um quadrado de porcelana, um rolo de papel de arroz, pincel e tintas e disse para ele viajar pelo mundo e anotar tudo que visse de belo e depois voltasse. O discípulo ficou tão emocionado com a tarefa que deixou cair o quadrado de porcelana partindo-o em 7 pedaços. O discípulo, tentando reproduzir o quadrado, percebeu uma imensidão de belas e conhecidas figuras feitas a partir das 7 peças. Assim, percebeu que não precisava mais correr o mundo, pois tudo que era belo poderia ser formado pelas 7 peças do Tangram.
Existem várias lendas sobre o surgimento do Tangram. Diz algumas escrituras que: uma pedra preciosa se desfez em sete pedaços e com eles era possível formar várias formas (animais, plantas, pessoas) outra diz que um imperador deixou o seu espelho cair, e esse se desfez em 7 pedaços que poderiam ser usados para formar várias figuras. A lenda principal e mais difundida a respeito do surgimento do Tangram diz que no século XII um monge taoísta deu ao seu discípulo um quadrado de porcelana, um rolo de papel de arroz, pincel e tintas e disse para ele viajar pelo mundo e anotar tudo que visse de belo e depois voltasse. O discípulo ficou tão emocionado com a tarefa que deixou cair o quadrado de porcelana partindo-o em 7 pedaços. O discípulo, tentando reproduzir o quadrado, percebeu uma imensidão de belas e conhecidas figuras feitas a partir das 7 peças. Assim, percebeu que não precisava mais correr o mundo, pois tudo que era belo poderia ser formado pelas 7 peças do Tangram.
Além do aspecto lúdico do jogo, o Tangram pode ser explorado no ensino da Matemática. Ele pode ser utilizado em diferentes conteúdos como área, perímetro, razão, proporção, fração, multiplicação, divisão, semelhança, simetrias, transformações isométricas, etc. Pode ser explorado também em interdisciplinaridade com as Ciências, Artes e História. São inúmeras as possibilidades exploratórias do Tangram utilizando-se de material concreto de manipulação. No entanto, o uso do ambiente computacional pode ampliar ainda mais as potencialidades pedagógicas do Tangram.
Com as peças do Tangram pode-se, dentre outras possibilidades, explorar:
- a identificação, comparação, descrição, classificação e representação de figuras geométricas planas;
- as transformações geométricas, através de composição e decomposição de figuras planas;
- a equivalência de áreas;
- a aplicação do Teorema de Pitágoras.
Além disso, com as sete peças desse quebra-cabeça é possível montar cerca de 1700 figuras dentre animais, plantas, pessoas, objetos, letras, números e outros, tornando-o um material pedagógico bastante atraente.
Com as peças do Tangram pode-se, dentre outras possibilidades, explorar:
- a identificação, comparação, descrição, classificação e representação de figuras geométricas planas;
- as transformações geométricas, através de composição e decomposição de figuras planas;
- a equivalência de áreas;
- a aplicação do Teorema de Pitágoras.
Além disso, com as sete peças desse quebra-cabeça é possível montar cerca de 1700 figuras dentre animais, plantas, pessoas, objetos, letras, números e outros, tornando-o um material pedagógico bastante atraente.
Montar as letras do alfabeto utilizando o tangram pode ser uma atividade divertida e instrutiva. Você pode utilizar os exemplos abaixo para direcionar o trabalho de montagem:
Vários moldes e modelos de Tangram prontos para você imprimir! Clique na imagem para ampliá-la e bom divertimento!
Algumas das milhares possíveis figuras que você pode criar a partir da montagem do tangram:
Fontes:
Montando barcos com tangram:
Montando casas com tangram:
Montando peixes com tangram
Montando coelhos com tangram
Montando gatos com tangram
Montando pessoas com tangram
Montando pessoas em barcos com tangram
Outras idéias com tangram:
Matemática Mania
Centro Virtual Goeldi
Wikipedia
Carol Cruz
Várias sugestões de atividades utilizando o Tangram
O que o aluno poderá aprender com estas atividades:
Conhecer a origem do Tangram.
Explorar as caractéristicas físicas das peças do Tangram.
Compor e decompor figuras usando o Tangram.
Criar e ilustrar história utilizando o Tangram
Explorar livremente as peças do Tangram, identificando formas.
- Para iniciar o trabalho, é bom contar alguma história ou dar ciência do que é o Tangram, de como surgiu, de como ele funciona, etc. Para isto, você pode utilizar um texto, uma lenda, uma história em quadrinhos etc. Encontrei uma história em quadrinhos muito legal com a turma da Mônica em flash e a transformei em jpg. para colocar aqui:
Encontrei também dois textos sobre a Lenda do Tangram, que podem dar abertura às atividades:
E mais um texto muito divertido para dar início ao trabalho:
Ao final da historia pergunte se eles conhecem o nome das figuras que você encontrou.
Geralmente os alunos nomeiam com facilidade o triângulo e o quadrado (losango), já o paralelogramo, talvez eles não conheçam, sendo necessário você apresentar. Pode ser que os alunos apontem o quadrado como sendo um losango, mostre que realmente ele é um losango (quadrilátero com todos os lados de mesma medida), porém, como todos os ângulos são retos ele também é um quadrado.- Quem já conhecia esse jogo?
- Qual é o nome do jogo?
- Como se joga?
- Será que o Tangram é uma invensão dos chineses?
2. É uma boa sugestão assistir a um vídeo sobre o assunto com a turma:
3. Você pode montar um texto coletivo com a turma sobre o tangram, para saber o que eles aprenderam sobre o assunto. Encontrei um modelinho muito legal:
3. Uma sugestão muito divertida e legal é apresentar os moldes, fornecer pedaços de cartolina colorida ou outro papel firme qualquer e deixar que eles criem seu próprio tangram:
4. Uma sugestão: Pedir que montem um quadrado, utilizando as peças embaralhadas do tangram.
5. É uma idéia interessante sugerir que montem textos, utilizando otangram. Ou seja, os alunos criam um pequeno texto e algumas palavras do mesmo são substituídas por figuras montadas por eles com o tangram:
Proponha a produção de uma história coletiva com figuras montandas com as peças do Tangram. Na produção dessa história, as crianças devem pensar nos personagens, o lugar onde acontecem as situações, as ações dos personagens. Lembre as crianças que a história deve ter uma seguência lógica. As crianças sugerem ações que se passam no início da história, os conflitos enfrentados pelos personagens e a solução final, ou seja, como termina a história. Veja o exemplo de uma atividade:
Fonte: Relatório da Prática Pedagógica. Turma do 1º ano B. NEI-CAp/UFRN.2008.
Leve os alunos ao laboratório de informática e peça que acessem o site: Jogar Tangram Online. (http://nlvm.usu.edu/en/nav/frames_asid_291_g_4_t_3.html).
Dê um tempo para que eles se familiarizem com o programa. Mostre-lhes que eles poderão girar as formas colocando o mouse nos cantos das figuras onde aparecerá um ponto no qual, segurando com o mouse, pode-se girar a forma. Para rotacionar a forma devem selecioná-la e clicar no primeiro botão do lado direito . Além disso, eles poderão colorir as formas como quiserem, para isso, basta selecionar uma forma e a cor desejada no menu do lado direito.
Após conhecerem o programa, peça para que eles identifiquem as formas geométricas nomeando-as verbalmente. A seguir peça para que as agrupe de acordo com as mesmas características. Provavelmente eles irão fazer dois grupos um de triângulos e outro de quadrilátero, ou três um com triângulos, um com o quadrado e outro com o paralelogramo. Questione quais os critérios utilizados para a classificação.
No caso dos dois grupos, é bem provável que a classificação tenha sido pelo número de lados. Já se fizeram três grupos eles podem ter usado os nomes, triângulos, quadrado e paralelogramo, para classificar. Se as duas classificações aparecerem, pergunte se existe alguma semelhança e/ou diferença nas classificações e qual delas seria a mais adequada para usar na classificação das figuras geométricas usando a nomenclatura pelo número de lados (triângulo e quadrilátero).
Caso só apareça a classificação em três grupos, questione se eles podem fazer de outra forma, usando apenas o número de lados. Assim, você estará induzindo-os a classificar pelo número de lados.
Leve-os a compreender que o paralelogramo é um quadrilátero assim como o quadrado. Aproveite esse momento para mostrar as características dos triângulos e dos quadriláteros.
Após conhecerem o programa, peça para que eles identifiquem as formas geométricas nomeando-as verbalmente. A seguir peça para que as agrupe de acordo com as mesmas características. Provavelmente eles irão fazer dois grupos um de triângulos e outro de quadrilátero, ou três um com triângulos, um com o quadrado e outro com o paralelogramo. Questione quais os critérios utilizados para a classificação.
No caso dos dois grupos, é bem provável que a classificação tenha sido pelo número de lados. Já se fizeram três grupos eles podem ter usado os nomes, triângulos, quadrado e paralelogramo, para classificar. Se as duas classificações aparecerem, pergunte se existe alguma semelhança e/ou diferença nas classificações e qual delas seria a mais adequada para usar na classificação das figuras geométricas usando a nomenclatura pelo número de lados (triângulo e quadrilátero).
Caso só apareça a classificação em três grupos, questione se eles podem fazer de outra forma, usando apenas o número de lados. Assim, você estará induzindo-os a classificar pelo número de lados.
Leve-os a compreender que o paralelogramo é um quadrilátero assim como o quadrado. Aproveite esse momento para mostrar as características dos triângulos e dos quadriláteros.
A seguir coloque os seguintes problemas:
- “Com quais peças podemos cobrir o quadrado?”
- “Com quais peças podemos cobrir o triângulo maior?”
- “E o paralelogramo?”
- “Usando apenas o triângulo menor, quantos são necessários para cobrir o quadrado, o triângulo médio, o triângulo maior e o paralelogramo?”
A seguir desafie-os a montar o quadrado inicial da historia que contou em sala, par isso, eles poderão usar um modelo que se encontra no menu no inferior da página.
Depois deixe que selecionem algumas figuras modelos que são dadas no programa e tentem completá-la com as peças do Tangram.
Professor, nessa aula, você estará desafiando os alunos a compor figuras usando as peças do Tangram com criatividade. (Fonte desta atividade da informática: Portal do Professor)
7.Convide seus alunos a criarem uma história em quadrinhos utilizando as peças do tangram, desenhando os balões e escrevendo as falas. As ilustrações serão feitas com o tangram! Vai ficar lindo!
Uma sugestão é que montem no tangram virtual as peças que desejarem e em seguida salvem cada peça feita utilizando a tecla print screen e o paint. Podem criar uma história em quadrinhos no computador utilizando o paint e as imagens salvas por eles.
9. Montagem de um Portfolio com as diversas peças criadas pelos alunos com o tangram colorido que eles montaram com cartolina. Fica lindo!
10. Montar um mural para exposição das atividades, imagens, desenhos, montagens feitas pelos alunos utilizando o tangram.
As imagens acima são do mural confeccionado pela professora Sonia, com os alunos do 4° ano do ensino fundamental, no Núcleo Escolar Municipal Juliana Tomporoski Krull.
11. Montar a lenda da descoberta do Tangram com o próprio tangram. Observe como ficou a atividade abaixo:
Atividade realizada pelo 4° ano do ensino fundamental da E.B.1 de Loureiro
Se você copiar, dê os créditos.