Jogos Matemáticos que eu uso em sala, e outros jogos legais
Ábaco
O cartaz valor lugar, abreviadamente chamado de cavalu pode ser usado no trabalho com números (sistema de numeração) e operações. De fácil confecção o cavalu, pode ser confeccionado colando-se uma folha de papel pardo pregueado (cada prega pode ter aproximadamente a profundidade de 3 centímetros) sobre um pedaço de papelão ou uma folha de papel cartão. Depois deve-se fazer duas separações verticais, usando para isso fitas, durex colorido ou até mesmo tiras de papel colorido. Com esse cartaz e alguns palitos, pode-se representar os números no sistema posicional além de realizar principalmente as operações de adição e subtração.
Por ser um material de fácil confecção, cada aluno pode confeccionar o seu próprio cavalu.
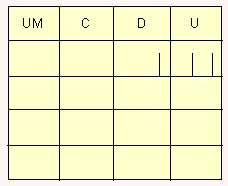
A seguir apresentamos o cavalu representando o número 12:
Atividades propostas:
O cavalu é um material que pode ser utlizado como variação para atividades de Sistema de Numeração. Por isso, sugerimos, como atividades introdutórias, as mesmas realizadas com oábaco e com o material dourado.
Para uma variação posterior, podem ser propostas atividades com a ordem do milhar, que foram pouco exploradas nos outros materiais.

QUE FIGURA É ESSA?
Objetivos:
Desenvolver a percepção visual de formas geométricas planas;
Comparar, ampliar e reduzir formas e figuras;
Fazer uso de nomenclatura adequada às formas;
Trabalhar com perímetro, lados e vértices.
Usar régua para desenhar.
Material:
Geoplano
Elásticos
Material para registro escrito.
Metodologia:
Esta atividade pode ser realizada em grupo, em duplas, ou individualmente.
O professor mostra uma forma já conhecida, pelo menos visualmente, ou seja, que eles conheçam e possam reproduzir, mesmo sem saber nomeá-las (quadrado, retângulo, trapézio, paralelogramo, hexágono, etc.)
No geoplano, usando 1 elástico, deverão reproduzi-la.
O professor pode sugerir que a figura deve ser montada utilizando um n.º de pregos. (se a figura mostrada estiver desenhada na malha pontilhada, facilitará a visualização da quantidade de pregos.)
Com a figura montada, o professor questiona o nome da figura; quantos lados ela tem; quantos pregos ela está tocando (possibilitando um 1º contato com a noção de perímetro).
A seguir, pergunta o que é preciso fazer para que essa figura fique maior.
Deixando-os explorar o geoplano, eles irão deslocar os elásticos para ampliá-la. Depois, pode pedir que a diminuam.
Daí, podem surgir questionamentos sobre quantos pregos foram usados na figura maior, e na menor, o que houve com as figuras – se ficaram iguais ou mudaram a forma.
Todas as questões podem ser registradas, e num segundo momento, as figuras formadas, desenhadas em quadriculados.




 eu adorrrrooo jogar isso! Jogo de Carta bom para a família toda, é relativamente barato se comparado a brinquedos de qualidade! Custa em média uns 30 reias, mas vale a pena viu contagia a família toda!
eu adorrrrooo jogar isso! Jogo de Carta bom para a família toda, é relativamente barato se comparado a brinquedos de qualidade! Custa em média uns 30 reias, mas vale a pena viu contagia a família toda!
6. Háaa o jogo de cartas 21
Que bate o jogo quem formar 21 ou chegar mais próximo, sem estourar (passar)
7.Rummikub(Grow / 2 a 4 jogadores)Excelente jogo, baseado no jogo de cartas Mexe-Mexe. A base do jogo é o jogo de buraco, mas aqui os jogos não são de ninguém. O desafio é se livrar de suas cartas, conseguindo manter os jogos da mesa sempre coerentes com as regras. Um desafio de raciocínio. As fichas plásticas facilitam os procedimentos. É um dos jogos mais vendidos no mundo
8.*Tô paquerando com esse jogo* Eu querooooooo!
Jenga
Nesse envolvente jogo de destreza da Hasbro, todos vão ficar na ponta da cadeira, ansiosos pelo próximo passo. O desafio é retirar blocos da base para o topo da torre, que vai ficando cada vez mais instável. Sucesso nos Estados Unidos, já apareceu no Brasil com o nome de Torremoto.
9.Vários jogos de tabuleiro tradicionais também ajudam na matématica, nem precisa ser um XADREZ, já vale uma dama, ludo, seí lá aqueles kits de jogos tradicionais que nem são caros mas que refoçam a estratégia e com isso o raciocínio lógico matemático
Dica de Blog que descobri e achei bacana, menções honrosas e agradecimentos: Ludo Mania Os jogos Mais legais



Teve origem provavelmente na Mesopotâmia, há mais de 5.500 anos. O ábaco pode ser considerado como uma extensão do ato natural de se contar nos dedos. Emprega um processo de cálculo com sistema decimal, atribuindo a cada haste um múltiplo de dez. Ele é utilizado ainda hoje para ensinar às crianças as operações de somar e subtrair.
JOGO DO NUNCA 10 (DEZ)
JOGO DO NUNCA 10 (DEZ)
Eu prefiro no ábaco aberto esse que está ai em cima:
Nunca 10
Objetivos:
- Construir o significado de Sistema de Numeração Decimal explorando situações-problema que envolvam contagem;
- Compreender e fazer uso do valor posicional dos algarismos, no Sistema de Numeração Decimal.
Material:
Ábaco de pinos – 1 por aluno
2 dados por grupo
Metodologia:
Os alunos divididos em grupos deverão, cada um na sua vez, pegar os dois dados e jogá-los, conferindo o valor obtido. Este valor deverá ser representado no ábaco. Para representá-lo deverão ser colocadas argolas correspondentes ao valor obtido no primeiro pino da direita para a esquerda (que representa as unidades). Após todos os alunos terem jogado os dados uma vez, deverão jogar os dados novamente, cada um na sua vez.
Quando forem acumuladas 10 argolas (pontos) no pino da unidade, o jogador deve retirar estas 10 argolas e trocá-las por 1 argola que será colocada no pino seguinte, representando 10 unidades ou 1 dezena. Nas rodadas seguintes, os jogadores continuam marcando os pontos, colocando argolas no primeiro pino da esquerda para a direita (casa das unidades), até que sejam acumuladas 10 argolas que devem ser trocadas por uma argola que será colocada no pino imediatamente posterior, o pino das dezenas.
Vencerá quem colocar a primeira peça no terceiro pino, que representa as centenas.
Com esta atividade inicial, é possível chamar a atenção dos alunos para o fato do agrupamento dos valores, e que a mesma peça tem valor diferente de acordo com o pino que estiver ocupando.
Possivelmente seja necessário realizar esta atividade mais de uma vez. É importante que os alunos possam registrá-la em seus cadernos, observando as estratégias e os pontos obtidos por cada um dos jogadores, etc.
Contando os objetos
Objetivos:
- Realizar contagens, utilizando a correspondência biunívoca (um a um);
- Construir o significado de Sistema de Numeração Decimal explorando situações-problema que envolvam contagem;
- Compreender e fazer uso do valor posicional dos algarismos, no Sistema de Numeração Decimal.
Material:
objetos
ábaco de pinos (1 por aluno)
Metodologia:
Poderão ser selecionados na classe objetos (lápis de cor, giz, pedaços coloridos de papel, borrachas, etc.) em quantidades superiores a 10 unidades, ou poderá ser pedido aos alunos que tragam objetos (bolinhas de gude, figurinhas, botões, tampinhas, moedas, etc.) de casa para montar uma "coleção". Os alunos deverão contar esses objetos, a princípio um a um, registrando a quantidade obtida no ábaco (lembrando que não podem deixar mais de 10 argolas num mesmo pino). Posteriormente, os alunos deverão encontrar outras formas de contar a quantidade de objetos que possuem. Pode-se propor ou aceitar contagens de 2 em 2, de 3 em 3, de 4 em 4..., até que os alunos percebam que quando têm quantidades maiores que 10, podem registrá-las diretamente no pino das dezenas.
Operações
Objetivos:
- Compreender e utilizar as técnicas operatórias para adição e subtração com trocas e reservas;
- Compreender e fazer uso das regras do Sistema de Numeração Decimal;
- Fazer uso de material semi simbólico para registro de cálculos de adição e subtração;
Objetivos:
- Construir o significado de Sistema de Numeração Decimal explorando situações-problema que envolvam contagem;
- Compreender e fazer uso do valor posicional dos algarismos, no Sistema de Numeração Decimal.
Material:
Ábaco de pinos – 1 por aluno
2 dados por grupo
Metodologia:
Os alunos divididos em grupos deverão, cada um na sua vez, pegar os dois dados e jogá-los, conferindo o valor obtido. Este valor deverá ser representado no ábaco. Para representá-lo deverão ser colocadas argolas correspondentes ao valor obtido no primeiro pino da direita para a esquerda (que representa as unidades). Após todos os alunos terem jogado os dados uma vez, deverão jogar os dados novamente, cada um na sua vez.
Quando forem acumuladas 10 argolas (pontos) no pino da unidade, o jogador deve retirar estas 10 argolas e trocá-las por 1 argola que será colocada no pino seguinte, representando 10 unidades ou 1 dezena. Nas rodadas seguintes, os jogadores continuam marcando os pontos, colocando argolas no primeiro pino da esquerda para a direita (casa das unidades), até que sejam acumuladas 10 argolas que devem ser trocadas por uma argola que será colocada no pino imediatamente posterior, o pino das dezenas.
Vencerá quem colocar a primeira peça no terceiro pino, que representa as centenas.
Com esta atividade inicial, é possível chamar a atenção dos alunos para o fato do agrupamento dos valores, e que a mesma peça tem valor diferente de acordo com o pino que estiver ocupando.
Possivelmente seja necessário realizar esta atividade mais de uma vez. É importante que os alunos possam registrá-la em seus cadernos, observando as estratégias e os pontos obtidos por cada um dos jogadores, etc.
Contando os objetos
Objetivos:
- Realizar contagens, utilizando a correspondência biunívoca (um a um);
- Construir o significado de Sistema de Numeração Decimal explorando situações-problema que envolvam contagem;
- Compreender e fazer uso do valor posicional dos algarismos, no Sistema de Numeração Decimal.
Material:
objetos
ábaco de pinos (1 por aluno)
Metodologia:
Poderão ser selecionados na classe objetos (lápis de cor, giz, pedaços coloridos de papel, borrachas, etc.) em quantidades superiores a 10 unidades, ou poderá ser pedido aos alunos que tragam objetos (bolinhas de gude, figurinhas, botões, tampinhas, moedas, etc.) de casa para montar uma "coleção". Os alunos deverão contar esses objetos, a princípio um a um, registrando a quantidade obtida no ábaco (lembrando que não podem deixar mais de 10 argolas num mesmo pino). Posteriormente, os alunos deverão encontrar outras formas de contar a quantidade de objetos que possuem. Pode-se propor ou aceitar contagens de 2 em 2, de 3 em 3, de 4 em 4..., até que os alunos percebam que quando têm quantidades maiores que 10, podem registrá-las diretamente no pino das dezenas.
Operações
Objetivos:
- Compreender e utilizar as técnicas operatórias para adição e subtração com trocas e reservas;
- Compreender e fazer uso das regras do Sistema de Numeração Decimal;
- Fazer uso de material semi simbólico para registro de cálculos de adição e subtração;
Material Escala Cuisenaire:
Quem inventou o material Cuisenaire?
Origem
O material cuisenaire foi criado pelo professor belga Georges Cuisenaire Hottelet (1891-1980) Esse ai ao lado depois de ter observado o desespero de um aluno, numa de suas aulas. Decidiu criar um material que ajudasse no ensino dos conceitos básicos da Matemática. Então cortou algumas réguas de madeira em 10 tamanhos diferentes e pintou cada peça de uma cor tendo assim surgido a Escala de Cuisenaire.
depois de ter observado o desespero de um aluno, numa de suas aulas. Decidiu criar um material que ajudasse no ensino dos conceitos básicos da Matemática. Então cortou algumas réguas de madeira em 10 tamanhos diferentes e pintou cada peça de uma cor tendo assim surgido a Escala de Cuisenaire.
Durante 23 anos, Cuisenaire estudou e experimentou o material que criara na aldeia belga de Thuin. Só 23 anos depois da sua criação (a partir de um encontro com outro professor – o egípcio Caleb Gattegno), é que o seu uso se difundiu com enorme êxito. O egípcio, radicado na Inglaterra, passou a divulgar o trabalho de Cuisenaire – a quem chamava de Senhor Barrinhas. Levou apenas 13 anos para passar a ser conhecido nas escolas de quase todo o mundo.
Feito originalmente de madeira, o Cuisenaire é constituído por modelos de prismas quadrangulares com alturas múltiplas da do cubo – representante do número 1 –em 10 cores diferentes e 10 alturas proporcionais.
Introdução
O material Cuisenaire é constituído por uma série de barras de madeira, sem divisão em unidades e com tamanhos variando de uma até dez unidades. Cada tamanho corresponde a uma cor específica.
Uma adaptação desse material pode ser a sua confecção em papel quadriculado, o que ressalta o número de unidades correspondente a cada cor:
O material cuisenaire foi criado pelo professor belga Georges Cuisenaire Hottelet (1891-1980) Esse ai ao lado
 depois de ter observado o desespero de um aluno, numa de suas aulas. Decidiu criar um material que ajudasse no ensino dos conceitos básicos da Matemática. Então cortou algumas réguas de madeira em 10 tamanhos diferentes e pintou cada peça de uma cor tendo assim surgido a Escala de Cuisenaire.
depois de ter observado o desespero de um aluno, numa de suas aulas. Decidiu criar um material que ajudasse no ensino dos conceitos básicos da Matemática. Então cortou algumas réguas de madeira em 10 tamanhos diferentes e pintou cada peça de uma cor tendo assim surgido a Escala de Cuisenaire.Durante 23 anos, Cuisenaire estudou e experimentou o material que criara na aldeia belga de Thuin. Só 23 anos depois da sua criação (a partir de um encontro com outro professor – o egípcio Caleb Gattegno), é que o seu uso se difundiu com enorme êxito. O egípcio, radicado na Inglaterra, passou a divulgar o trabalho de Cuisenaire – a quem chamava de Senhor Barrinhas. Levou apenas 13 anos para passar a ser conhecido nas escolas de quase todo o mundo.
Feito originalmente de madeira, o Cuisenaire é constituído por modelos de prismas quadrangulares com alturas múltiplas da do cubo – representante do número 1 –em 10 cores diferentes e 10 alturas proporcionais.
Introdução
O material Cuisenaire é constituído por uma série de barras de madeira, sem divisão em unidades e com tamanhos variando de uma até dez unidades. Cada tamanho corresponde a uma cor específica.
Uma adaptação desse material pode ser a sua confecção em papel quadriculado, o que ressalta o número de unidades correspondente a cada cor:
Atividades Propostas
Construindo um muro
Objetivo:
- Introduzir a operação de adição e a comutatividade.
Material:
- Material Cuisenaire
Metodologia:
O professor pode apresentar uma barra e pedir que os alunos construam o resto do muro, usando sempre duas barras que juntas tenham o mesmo comprimento da peça inicial
As adições cujo total é dez ou maior que dez, assim como as adições com três ou mais parcelas podem ser introduzidas com essa atividade.
Construindo um muro especial
Objetivo:
- Introduzir o conceito de multiplicação, enquanto soma de parcelas iguais.
Material:
Material Cuisenaire
Metodologia:
O professor pode pedir aos alunos que formem muros usando, por exemplo:
2 tijolos pretos
4 tijolos vermelhos
5 tijolos roxos
Após a realização das atividades concretamente, professor pode pedir que os alunos registrem como fizeram a construção do muro e discutir com seus alunos as formas de registro.
Construindo um muro
Objetivo:
- Introduzir a operação de adição e a comutatividade.
Material:
- Material Cuisenaire
Metodologia:
O professor pode apresentar uma barra e pedir que os alunos construam o resto do muro, usando sempre duas barras que juntas tenham o mesmo comprimento da peça inicial
As adições cujo total é dez ou maior que dez, assim como as adições com três ou mais parcelas podem ser introduzidas com essa atividade.
Construindo um muro especial
Objetivo:
- Introduzir o conceito de multiplicação, enquanto soma de parcelas iguais.
Material:
Material Cuisenaire
Metodologia:
O professor pode pedir aos alunos que formem muros usando, por exemplo:
2 tijolos pretos
4 tijolos vermelhos
5 tijolos roxos
Após a realização das atividades concretamente, professor pode pedir que os alunos registrem como fizeram a construção do muro e discutir com seus alunos as formas de registro.
CARTAZ VALOR LUGAR (CAVALU) eu Chamo de QVL- Quadro de Valor e Lugar
O cartaz valor lugar, abreviadamente chamado de cavalu pode ser usado no trabalho com números (sistema de numeração) e operações. De fácil confecção o cavalu, pode ser confeccionado colando-se uma folha de papel pardo pregueado (cada prega pode ter aproximadamente a profundidade de 3 centímetros) sobre um pedaço de papelão ou uma folha de papel cartão. Depois deve-se fazer duas separações verticais, usando para isso fitas, durex colorido ou até mesmo tiras de papel colorido. Com esse cartaz e alguns palitos, pode-se representar os números no sistema posicional além de realizar principalmente as operações de adição e subtração.
Por ser um material de fácil confecção, cada aluno pode confeccionar o seu próprio cavalu.
A seguir apresentamos o cavalu representando o número 12:
Atividades propostas:
O cavalu é um material que pode ser utlizado como variação para atividades de Sistema de Numeração. Por isso, sugerimos, como atividades introdutórias, as mesmas realizadas com oábaco e com o material dourado.
Para uma variação posterior, podem ser propostas atividades com a ordem do milhar, que foram pouco exploradas nos outros materiais.
GEOPLANO:

O geoplano é um material criado pelo matemático inglês Calleb Gattegno. Constitui-se por uma placa de madeira, marcada com uma malha quadriculada ou pontilhada. Em cada vértice dos quadrados formados fixa-se um prego, onde se prenderão os elásticos, usados para "desenhar" sobre o geoplano. Podem-se criar geoplanos de vários tamanhos, de acordo com o n.º de pinos de seu lado, por exemplo, 5x5, ou seja, cada lado do geoplano tem 5 pinos (pregos).
Atividades PropostasQUE FIGURA É ESSA?
Objetivos:
Desenvolver a percepção visual de formas geométricas planas;
Comparar, ampliar e reduzir formas e figuras;
Fazer uso de nomenclatura adequada às formas;
Trabalhar com perímetro, lados e vértices.
Usar régua para desenhar.
Material:
Geoplano
Elásticos
Material para registro escrito.
Metodologia:
Esta atividade pode ser realizada em grupo, em duplas, ou individualmente.
O professor mostra uma forma já conhecida, pelo menos visualmente, ou seja, que eles conheçam e possam reproduzir, mesmo sem saber nomeá-las (quadrado, retângulo, trapézio, paralelogramo, hexágono, etc.)
No geoplano, usando 1 elástico, deverão reproduzi-la.
O professor pode sugerir que a figura deve ser montada utilizando um n.º de pregos. (se a figura mostrada estiver desenhada na malha pontilhada, facilitará a visualização da quantidade de pregos.)
Com a figura montada, o professor questiona o nome da figura; quantos lados ela tem; quantos pregos ela está tocando (possibilitando um 1º contato com a noção de perímetro).
A seguir, pergunta o que é preciso fazer para que essa figura fique maior.
Deixando-os explorar o geoplano, eles irão deslocar os elásticos para ampliá-la. Depois, pode pedir que a diminuam.
Daí, podem surgir questionamentos sobre quantos pregos foram usados na figura maior, e na menor, o que houve com as figuras – se ficaram iguais ou mudaram a forma.
Todas as questões podem ser registradas, e num segundo momento, as figuras formadas, desenhadas em quadriculados.
TANGRAN

O tangram é um quebra-cabeça chinês, de origem milenar. Ao contrário de outros quebra-cabeças ele é formado por apenas sete peças com as quais é possível criar e montar cerca de 1700 figuras entre animais, plantas, pessoas, objetos, letras, números, figuras geométricas e outros. As regras desse jogo consistem em usar as sete peças em qualquer montagem colocando-as lado a lado sem sobreposição.
Com o uso do tangram você pode trabalhar a identificação, comparação, descrição, classificação e desenho de formas geométricas planas., visualização e representação de figuras planas, exploração de transformações geométricas através de decomposição e composição de figuras, compreensão das propriedades das figuras geométricas planas, representação e resolução de problemas usando modelos geométricos. Esse trabalho permite o desenvolvimento de algumas habilidades tais como a visualização, percepção espacial, análise, desenho, escrita e construção. Se utilizado em terceiras e quartas séries pode envolver ainda noções de área e frações.
Este quebra-cabeça tem sido utilizado como material didático nas aulas de Artes e está cada vez mais presente nas de Matemática. O trabalho com o tangram deve em suas atividades iniciais visar a exploração das peças e a identificação das suas formas.Logo depois, se passa à sobreposição e construção de figuras dadas a partir de uma silhueta, nesse caso, cabe ao aluno reconhecer e interpretar o que se pede, analisar as possibilidades e tentar a construção. Durante todo esse processo, a criança precisa analisar as propriedades das peças do tangram e da figura que se quer construir, se detendo ora no todo de cada figura, ora nas partes.
Jogos que dispensam comentários:
1. Macaca ou Marelinha

Colaca- se os números nas casas, ou multiplos, triplos, resultados, enfim e a criança deve jogar a pedrinha na casa da resposta correta
2. Soma com dados (bozó)
Materiais:
Em educação pode -se usar quantos dados for o nível da turma:
Material:Um copo de arremesso – de preferência de couro
Dados comuns (bozó)Uma caderneta de anotação para cada Jogador (dupla).
Preparação:
Cada um coloca os dados no copinho de couro e emborca o copo na mesa, ou na rodinha e soma os pontos, a criança anota ganha quem tirar o número maior.
3. Bingo
O bingo é conhecido né??!! Os materiais são pedras numeradas até 80 e cartelas, milho, feijão ou outra coisa para marcar ganha quem preencher a cartela primeiro, é bem baratinho em centros comerciais acho que sai mais barato que fazer
4. Resta Um
Tem uns vendidos na feira de artesanato que tem o tabuleiro em pedra e os pinos são de bola de bude, bila, peteca! Chiquérrrrimos para dar de presente e por na mesa de centro da sala e nem são caros uns 25 reias!

Mas como é um jogo antigo também é vendido em casas de 1.99 que tanto pode jogar sozinho quanto em duplas, vc vai comendo as pinos até conseguir deixar a menor quantidade possível de pinos.
5.Can Can
Can-can é um jogo de cartas da Grow extremamente parecido com o Uno (Mattel) e o conhecido mau-mau (este último é jogado com cartas de baralho de 52 cartas).
 eu adorrrrooo jogar isso! Jogo de Carta bom para a família toda, é relativamente barato se comparado a brinquedos de qualidade! Custa em média uns 30 reias, mas vale a pena viu contagia a família toda!
eu adorrrrooo jogar isso! Jogo de Carta bom para a família toda, é relativamente barato se comparado a brinquedos de qualidade! Custa em média uns 30 reias, mas vale a pena viu contagia a família toda!6. Háaa o jogo de cartas 21
Que bate o jogo quem formar 21 ou chegar mais próximo, sem estourar (passar)
7.Rummikub(Grow / 2 a 4 jogadores)Excelente jogo, baseado no jogo de cartas Mexe-Mexe. A base do jogo é o jogo de buraco, mas aqui os jogos não são de ninguém. O desafio é se livrar de suas cartas, conseguindo manter os jogos da mesa sempre coerentes com as regras. Um desafio de raciocínio. As fichas plásticas facilitam os procedimentos. É um dos jogos mais vendidos no mundo
8.*Tô paquerando com esse jogo* Eu querooooooo!
Jenga

Nesse envolvente jogo de destreza da Hasbro, todos vão ficar na ponta da cadeira, ansiosos pelo próximo passo. O desafio é retirar blocos da base para o topo da torre, que vai ficando cada vez mais instável. Sucesso nos Estados Unidos, já apareceu no Brasil com o nome de Torremoto.
9.Vários jogos de tabuleiro tradicionais também ajudam na matématica, nem precisa ser um XADREZ, já vale uma dama, ludo, seí lá aqueles kits de jogos tradicionais que nem são caros mas que refoçam a estratégia e com isso o raciocínio lógico matemático
Dica de Blog que descobri e achei bacana, menções honrosas e agradecimentos: Ludo Mania Os jogos Mais legais




Nenhum comentário:
Postar um comentário